PyTorch中设置学习率衰减的方法／torch.optim.lr_scheduler／learning_rate_decay

时间：2024-04-22 14:33:14

我们都知道几乎所有的神经网络采取的是梯度下降法来对模型进行最优化，其中标准的权重更新公式：

$W+=\\alpha * gradient$

学习率 $\\alpha$ 控制着梯度更新的步长(step)， $\\alpha$ 越大，意味着下降的越快，到达最优点的速度也越快，如果为0，则网络就会停止更新
学习率过大，在算法优化的前期会加速学习，使得模型更容易接近局部或全局最优解。但是在后期会有较大波动，甚至出现损失函数的值围绕最小值徘徊，波动很大，始终难以达到最优。所以引入学习率衰减的概念，直白点说，就是在模型训练初期，会使用较大的学习率进行模型优化，随着迭代次数增加，学习率会逐渐进行减小，保证模型在训练后期不会有太大的波动，从而更加接近最优解

大致可以分为两类：

根据先验知识进行人为设定，达到多少轮之后，将学习率改为固定的值
随着epoch的增加，学习率按照一定方式自动发生衰减

import torch
import matplotlib.pyplot as plt
%matplotlib inline
from torch.optim import *
import torch.nn as nn
class net(nn.Module):
    def __init__(self):
        super(net,self).__init__()
        self.fc = nn.Linear(1,10)
    def forward(self,x):
        return self.fc(x)
model = net()
LR = 0.01
optimizer = Adam(model.parameters(),lr = LR)
lr_list = []
for epoch in range(100):
    if epoch % 5 == 0:
        for p in optimizer.param_groups:
            p['lr'] *= 0.9
    lr_list.append(optimizer.state_dict()['param_groups'][0]['lr'])
plt.plot(range(100),lr_list,color = 'r')

lr_scheduler.LambdaLR(optimizer, lr_lambda, last_epoch=-1, verbose=False)

更新策略：将每个参数组的学习率设置为初始lr乘以给定函数。当last_epoch=-1时，将初始lr设置为lr
参数

optimizer(Optimizer)：要更改学习率的优化器
lr_lambda(function or list)：给定整数参数epoch计算乘数的函数，或者是list形式的函数，分别计算各个parameter groups的学习率更新用到的λ
last_epoch(int)：最后一个epoch的index，默认值为-1。如果是训练了很多个epoch后中断了，继续训练，这个值就等于加载的模型的epoch。默认为-1表示从头开始训练，即从epoch=1开始
verbose(bool)：True的话为每次更新打印一个stdout，默认为False

注意：
在将optimizer传给scheduler后，在shcduler类的__init__方法中会给optimizer.param_groups列表中的那个元素（字典）增加一个key="initial_lr"的元素表示初始学习率，等于optimizer.defaults['lr']。

使用示例

optimizer_1 = torch.optim.Adam(net_1.parameters(), lr = initial_lr)
scheduler_1 = LambdaLR(optimizer_1, lr_lambda=lambda epoch: 1/(epoch+1))
# train
print("第%d个epoch的学习率：%f" % (epoch, optimizer_1.param_groups[0]['lr']))
scheduler_1.step()
# -----------------使用示例2------------------
import numpy as np 
lr_list = []
model = net()
LR = 0.01
optimizer = Adam(model.parameters(),lr = LR)
lambda1 = lambda epoch:np.sin(epoch) / epoch
scheduler = lr_scheduler.LambdaLR(optimizer,lr_lambda = lambda1)
for epoch in range(100):
    scheduler.step()
    lr_list.append(optimizer.state_dict()['param_groups'][0]['lr'])
plt.plot(range(100),lr_list,color = 'r')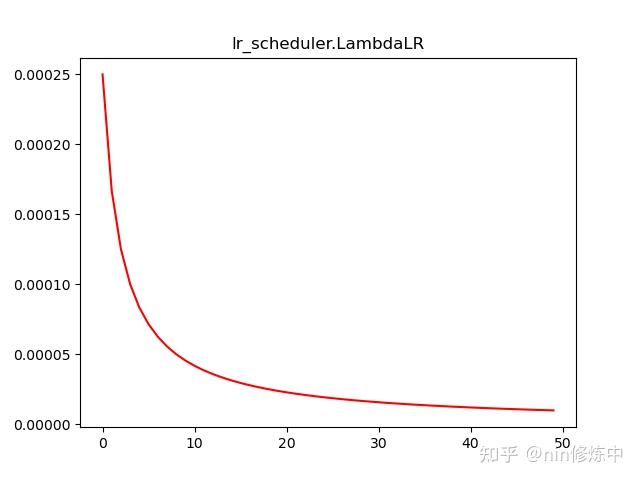

torch.optim.lr_scheduler.StepLR(optimizer, step_size, gamma=0.1, last_epoch=-1)

更新策略：每经过step_size 个epoch，做一次学习率decay，以gamma值为缩小倍数。

注意：此函数产生的decay效果，可能与函数外部的对于学习率的更改同时发生，当last_epoch=-1时，将初始lr设置为Ir。

optimizer（Optimizer）：要进行学习率decay的优化器
step_size（int）：每经过step_size 个epoch，做一次学习率decay
gamma（float）：学习率衰减的乘法因子。Default：0.1
last_epoch（int）：最后一个epoch的index。Default：0.1
verbose（bool）：如果为True，每一次更新都会打印一个标准的输出信息，Default：False

lr_list = []
model = net()
LR = 0.01
optimizer = Adam(model.parameters(),lr = LR)
scheduler = lr_scheduler.StepLR(optimizer,step_size=5,gamma = 0.8)
for epoch in range(100):
    scheduler.step()
    lr_list.append(optimizer.state_dict()['param_groups'][0]['lr'])
plt.plot(range(100),lr_list,color = 'r')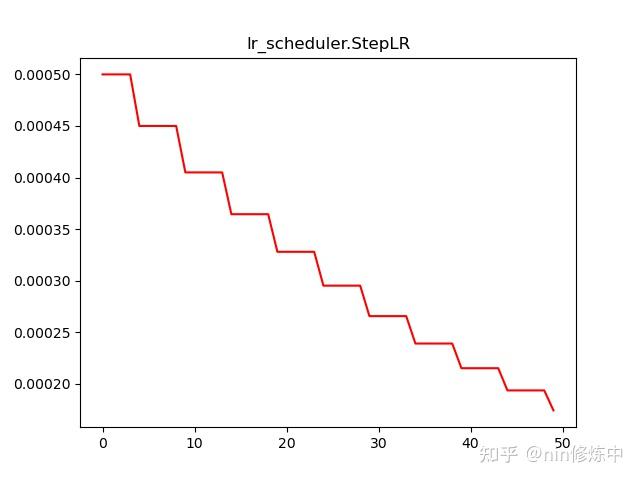

torch.optim.lr_scheduler.MultiStepLR(optimizer, milestones, gamma=0.1, last_epoch=-1, verbose=False)

**更新策略：**一旦达到某一阶段(milestones)时，就可以通过gamma系数降低每个参数组的学习率。

注意：此函数产生的decay效果，可能与函数外部的对于学习率的更改同时发生，当last_epoch=-1时，将初始lr设置为Ir

optimizer（Optimizer）：要进行学习率decay的优化器
milestones（list）：epoch索引列表，必须是升序排列
gamma（float）：学习率衰减的乘法因子。Default：0.1
last_epoch（int）：最后一个epoch的index。Default：0.1
verbose（bool）：如果为True，每一次更新都会打印一个标准的输出信息，Default：False

可以按照milestones列表中给定的学习率，进行分阶段式调整学习率

lr_list = []
model = net()
LR = 0.01
optimizer = Adam(model.parameters(),lr = LR)
scheduler = lr_scheduler.MultiStepLR(optimizer,milestones=[20,80],gamma = 0.9)
for epoch in range(100):
    scheduler.step()
    lr_list.append(optimizer.state_dict()['param_groups'][0]['lr'])
plt.plot(range(100),lr_list,color = 'r')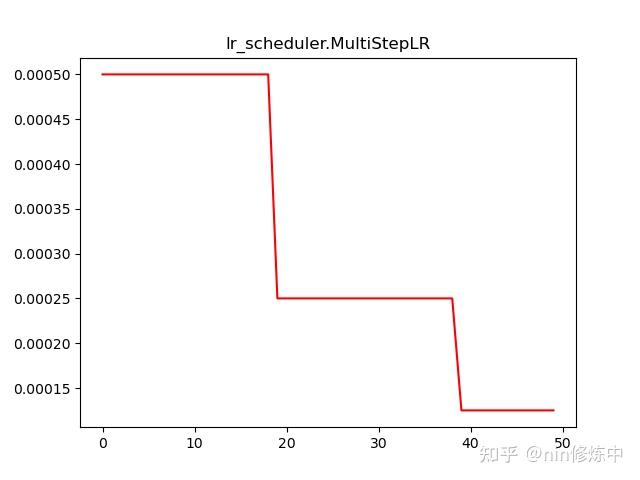

torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma, last_epoch=-1, verbose=False)

更新策略：每一次epoch，lr都乘gamma

optimizer（Optimizer）：要进行学习率decay的优化器
gamma（float）：学习率衰减的乘法因子。Default：0.1
last_epoch（int）：最后一个epoch的index。Default：0.1
verbose（bool）：如果为True，每一次更新都会打印一个标准的输出信息，Default：False

lr_list = []
model = net()
LR = 0.01
optimizer = Adam(model.parameters(),lr = LR)
scheduler = lr_scheduler.ExponentialLR(optimizer, gamma=0.9)
for epoch in range(100):
    scheduler.step()
    lr_list.append(optimizer.state_dict()['param_groups'][0]['lr'])
plt.plot(range(100),lr_list,color = 'r')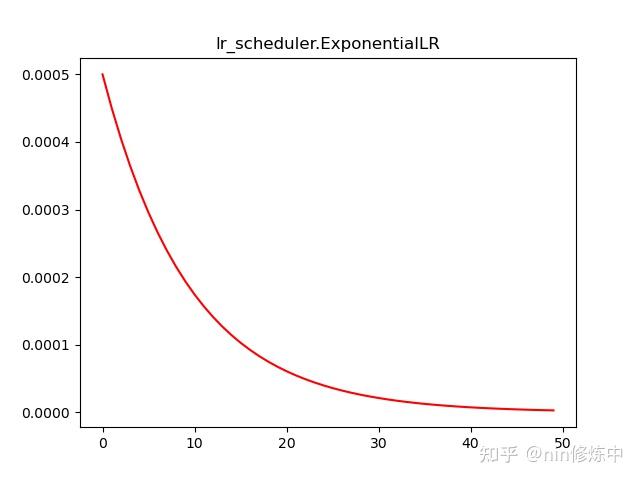

torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max, eta_min=0, last_epoch=-1, verbose=False)

更新策略：按照余弦波形的衰减周期来更新学习率，前半个周期从最大值降到最小值，后半个周期从最小值升到最大值

optimizer（Optimizer）：要进行学习率decay的优化器
T_max （int）：余弦波形周期的一半，比如T_max=10，则学习率衰减周期为20，其中前半段即前10个周期学习率从最大值降到最小值，后10个周期从最小值升到最大值
eta_min（float）：学习率衰减的最小值，Default：0
last_epoch（int）：最后一个epoch的index。Default：0.1
verbose（bool）：如果为True，每一次更新都会打印一个标准的输出信息，Default:False

lr_list = []
model = net()
LR = 0.01
optimizer = Adam(model.parameters(),lr = LR)
scheduler = lr_scheduler.CosineAnnealingLR(optimizer, T_max = 20)
for epoch in range(50):
    scheduler.step()
    lr_list.append(optimizer.state_dict()['param_groups'][0]['lr'])
plt.plot(range(100),lr_list,color = 'r')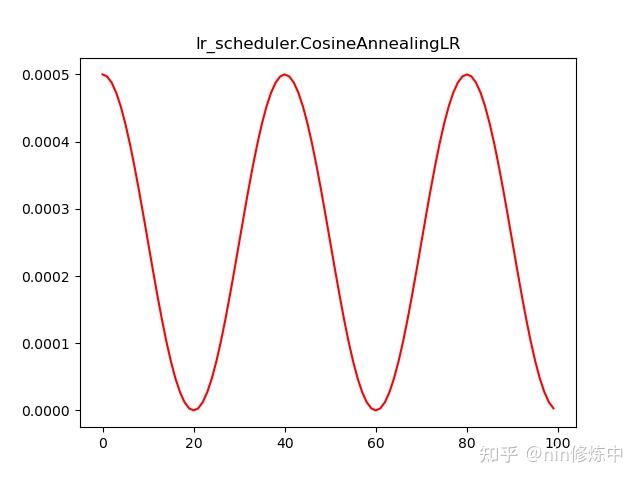

参考链接：